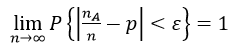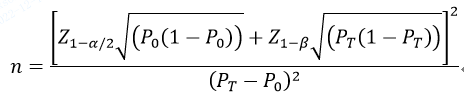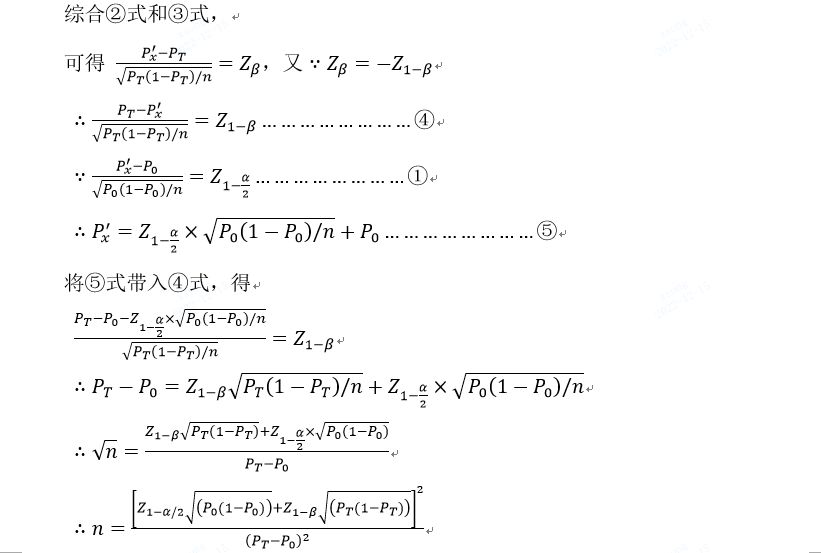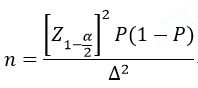国家药品监督管理局发布的《体外诊断试剂临床试验技术指导原则》(2021年第72号通告)(下文简述指导原则)中,给出了有确定的临床可接受标准和不设定临床可接受标准的两种情况下估算样本量的方法和公式,为体外诊断试剂临床试验计算样本量提供了依据,成为临床试验方案设计与统计学考量的重要因素之一。但是目前一般是直接使用公式,对公式建立的依据缺乏了解,为了加强对上述公式底层逻辑的了解,做到知其然,也知其所以然,更好地利用公式,下面对这两种情况下的估算公式的建立依据和推导过程进行解析。对于定性体外诊断试剂的临床试验,从统计学的角度出发,根据伯努利大数定律
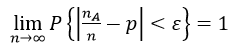
样本量越趋近于无穷大越能越能真实反应试剂的性能,同时可以减少范Ⅰ类错误α(消费者风险)或Ⅱ类错误β(研究者风险)的风险。但是实际临床试验过程中出于成本和时间等因素的考虑,企业不希望也不可能做到无穷大的样本量。因此,一般情况下,制造商在进行临床试验设计时为满足试剂的临床性能的要求,通过统计分析确定一定样本量和检测结果数学期望的效应值可以满足Ⅰ类错误概率α或Ⅱ类错误概率β的设定即可。
有临床可接受标准的样本量估算
指导原则中第1个举例是需证明产品评价指标满足评价指标预期值且优于临床可接受标准要求情况下的最低样本量估算方法,公式为
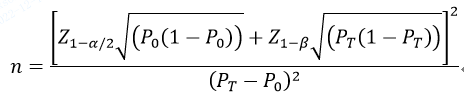
公式中,n为样本量;Z1-α/2、Z1-β为显著性水平和把握度的标准正态分布的分数位,P0为评价指标的临床可接受标准,PT为试验体外诊断试剂评价指标预期值。

这里的逻辑需要解释一下,如下图所示,Ⅱ类错误β是指原假设H0为假但被接受的概率,即假阴性,也就是说存在Ⅱ类错误时就不存在犯Ⅰ类错误的说法。但为了根据检验效能(1-β)计算样本量就需要得到H0的拒绝域,即下图中橙色面积,所以我们虽然预期H0不成立但只能先假设H0成立。在例1中,Ⅱ类错误是指产品效应值符合评价指标预期值,却仅仅认为效应值满足临床可接受标准,即图中蓝色面积。根据给定的Ⅱ类错误概率β计算的检验效能1-β即图中蓝色斜线部分的面积,此例中检验效能的意义是临床可接受标准为假而拒绝临床可接受标准,从而选择评价指标预期值的概率。了解计算思路后我们开始进行最低样本量计算公式的推导。
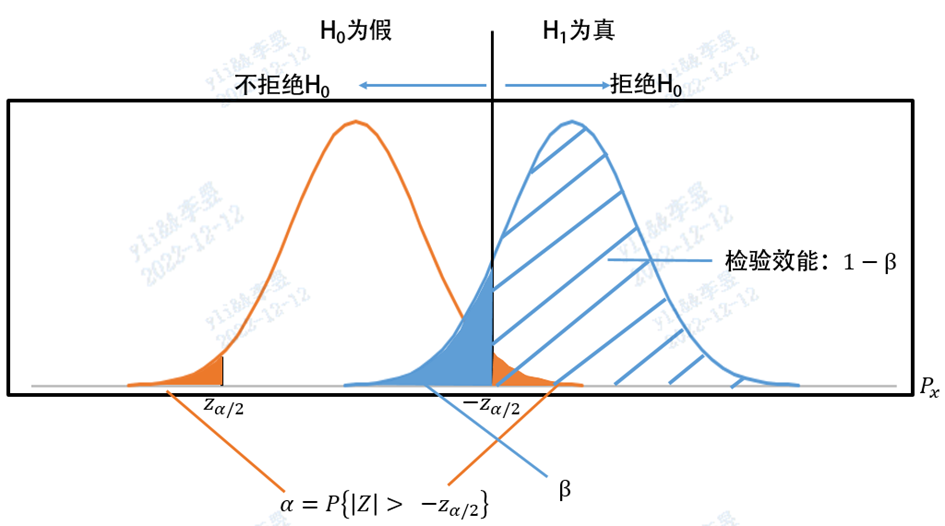


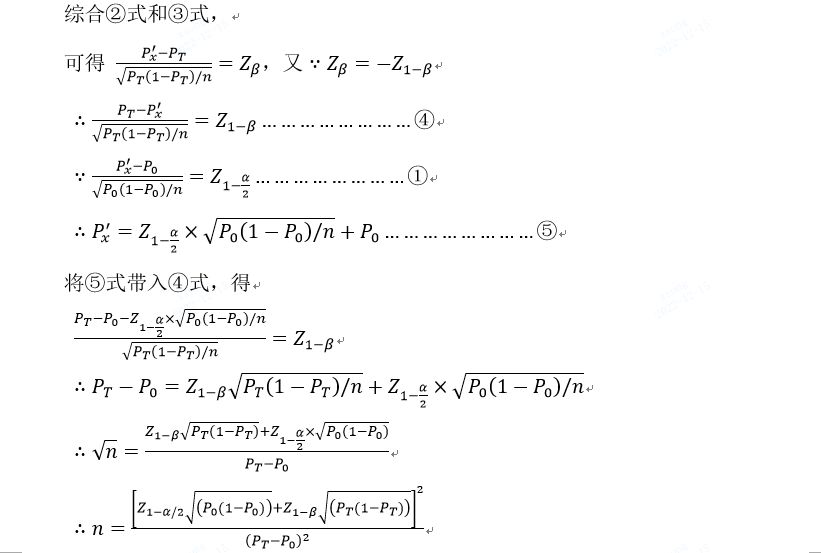
此时计算所得n值是在取Z1-α/2、Z1-β的临界状态下的样本量,因为显著性水平和把握度均会随着样本量的增加而增大,因此临床试验的样本量应不低于n值且应尽量增加以更真实反应试剂性能。
没有临床可接受标准的样本量估算
指导原则中第2个举例是只保证评价指标满足期望精度水平(置信区间的宽度一定),而不设定临床可接受标准的情况下最低样本量的计算方法,公式为
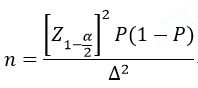


这里需要注意的是,因为⑥式中固定了Δ和显著水平1-α/2,因此估算的是最大的样本量,而不是最少的。当⑥式中的取最大值时,显著水平1-α/2下不拒绝H0的风险最高,或者说试验结果最可信。这里理解起来有些混淆,举个例子,我们的检测试剂灵敏度的期望是80%,如果我们只试验4次,灵敏度是75%,那我们会继续做更多的试验去进行验证;而如果我们试验了4000次,灵敏度是75%,直观上我们会更容易相信试剂的灵敏度确实达不到期望。实际上,效应值、检验水准(即α)和样本量三者是紧密相连的,其中之一发生变化,如果保持另一个不变,则第三个变量必定变化,从⑥式中也可以体现。临床试验过程中,我们往往是设置一个检验水准,再根据效应值和样本量去计算P值(假设检验统计量)并与检验水准进行比较,来检验效应值是否满足评价指标预期值。当临床试验样本量增加同时检验水准不变时,就需要效应值更接近评价指标预期值,即Δ更小。所以⑥式只是设定Δ情况下的样本估算量,只是一个参考值。如果实际临床试验时Δ小于设定值时,那么计算的样本量不是试验结果最可信情况;当Δ大于设定值时,可能会出现拒绝H0的情况。总之,指导原则中给出的估算公式是最低样本量的参考量,在此基础上应以临床性能得到充分评价为目标,尽可能的增加临床试验的样本量。
本文著作权属原创者所有,不代表本站立场。我们转载此文出于传播更多资讯之目的,如涉著作权事宜请联系删除。